Biography

I’m currently an assistant professor at the MAP5 laboratory and the STID departement of IUT de Paris, which is part of Université de Paris. I’ve done a PhD in AgroParisTech supervised by Céline Lévy-Leduc, Julien Chiquet and Laure Sansonnet. After thtat, I was in a postdoctoral position, between Sorbonne Université and Toulouse institut of mathematics, mentored by Etienne Roquain and Pierre Neuvial.

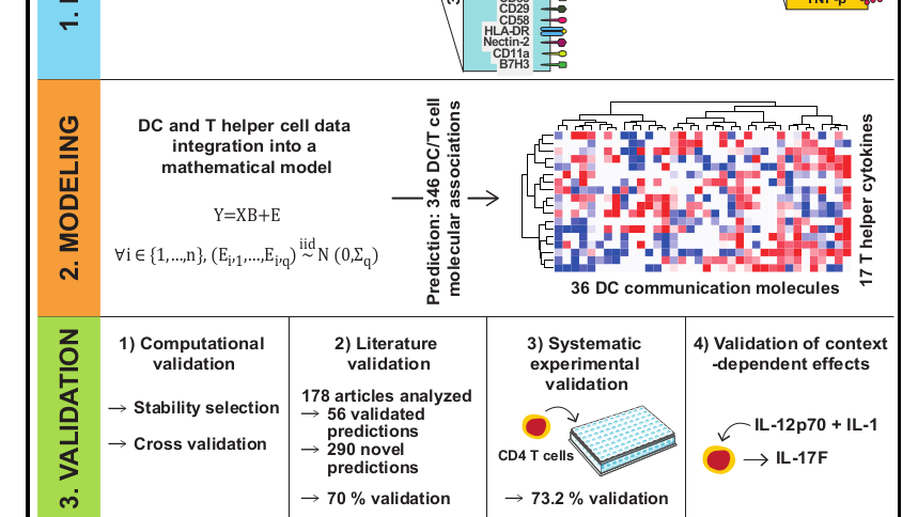
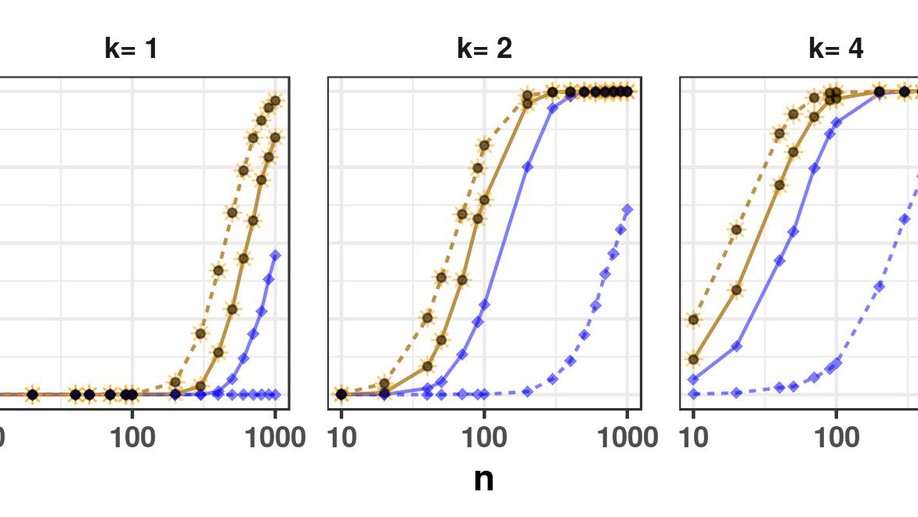
• Research: My PhD titled Regularized methods to study multivariate data in high dimensional settings : theory and applications aims at selecting variable of interest in the multivariate linear model when the number of responses is much higher than the sample size. My postdoc aims at finding upper bounds of the number of false discoveries for all the possible sets of selected variables in a multiple testing framework. These upper bounds have to be valid with high probabilities. Most of the existing bounds are too conservative and a crucial challenge is to build new post hoc bounds with better performances.

• Teaching:

  • During my PhD I have given 192 hours of directed works on statistical inference and linear modeling. The students were the first and second years of the engieneering school AgroParisTech.
  • During my postdoc I’ve given a 30 hours course on probabilities and statistics to the Master students of Polytech school of Paris.
  • Since 2020 I teach in IUT de Paris.

• Association As a member of the young group of the French statistical society I co-organised a meeting of the young European statistician, a session of the JDS (French statistical days) 2019, and one session and two workshops for the JDS 2020.